Question:
An electric dipole is formed by two charges $+q$ and $–q$ located in $xy-plane$ at $(0, 2)$ mm and $(0, –2)$ mm, respectively, as shown in the figure. The electric potential at point $P(100, 100)$ mm due to the dipole is $V_0$. The charges $+q$ and $–q$ are then moved to the points $(–1, 2)$ mm and $(1, –2)$ mm, respectively. What is the value of electric potential at P due to the new dipole ?
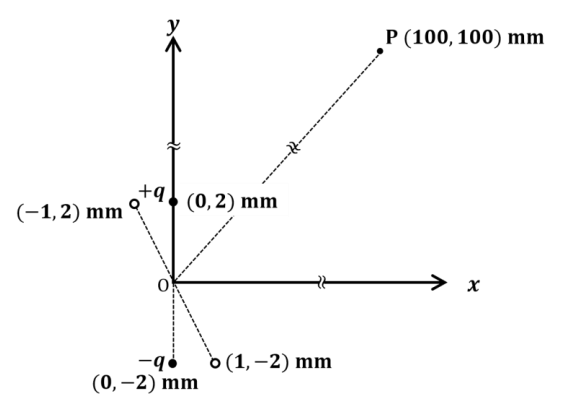
(A) $𝑉_0/4$
(B) $𝑉_0/2$
(C) $𝑉_0/√2$
(D) $3𝑉_0/4$
Solution:
Required Utensils:
- Vectors (Along with Coordinate Geometry)
- Formula for Electric Potential due to a Dipole i.e. $$V = \frac{K \vec P \cdot \vec r}{r^3}$$
- Where V is the potential due to the dipole
- K is Coulomb Constant
- $\vec P$ is Dipole moment
- $\vec r$ is the position vector
- $r$ is magnitude of vector $\vec r$
Preparation:
This is a comparison question, so no need to convert the units.
We will find potential in the two cases. First dipole with original position, then dipole with changed position.
We then divide first case with second and we got our desired result.
Case I:
$$\vec r = 100 \hat i + 100 \hat j$$
$$ r = 100 \sqrt{2}$$ No need to calculate magnitude of ‘r’ as it is same in both cases and will be cancelled
$$\vec P = q \vec a$$
Where $\vec a = 4 \hat j$ so $$\vec P = 4q \hat j$$
$$V_o = \frac{K \vec P \cdot \vec r}{r^3}$$
$$V_o = \frac{K (4q \hat j)\cdot (100 \hat i + 100 \hat j)}{r^3}$$
or
$$V_o = \frac{400Kq}{r^3}…………..(i)$$
Case II:
$\vec r$ is same in this case. Only thing which change in this case is $\vec a$
$$\vec a = (- \hat i + 2 \hat j) – ( \hat i – 2 \hat j)$$ or
$$\vec a = (-2 \hat i + 4 \hat j)$$
$$\vec P = q(-2 \hat i + 4 \hat j)$$
So $$V = \frac{Kq(-2 \hat i + 4 \hat j) \cdot (100 \hat i + 100 \hat j)}{r^3}$$
$$V = \frac{200Kq}{r^3}…………….(ii)$$
Dividing equation $(i)$ by equation $(ii)$, we get
$$\frac{V_o}{V} = 2$$
$$\Rightarrow V = \frac{V_o}{2}$$
Hence option (B) is the correct answer

Leave a Reply