If the refractive index of the material of a prism is $\cot \frac{A}{2}$, where A is the angle of prism then the angle of minimum deviation will be

If the refractive index of the material of a prism is $\cot \frac{A}{2}$, where A is the angle of prism then the angle of minimum deviation will be

(A) $\pi – 2A$

(B) $\frac{\pi}{2} – 2A$

(C) $\pi – A$

(D) $\frac{\pi}{2} – A$

Solution:

This question was asked in JEE-Mains 2024 on January 27, 2024 in the morning session.

Required Utensils:

1. Equation of Prism from NCERT

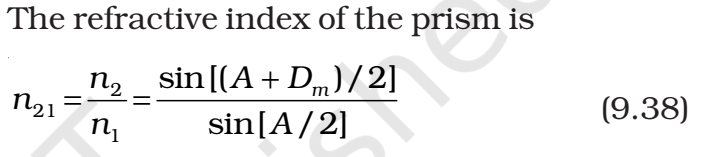
Preparation:

Given:

Refractive Index $= n = \cot \frac{A}{2} = \frac{\sin \frac{(A+D_m)}{2}}{\sin \frac{A}{2}}$

So, $\frac{\cos \frac{A}{2}}{\sin \frac{A}{2}} = \frac{\sin \frac{(A+D_m)}{2}}{\sin \frac{A}{2}}$

Or, $\cos \frac{A}{2} = \sin \frac{(A+D_m)}{2}$

Or, $\frac{(A+D_m)}{2} = \frac{\pi}{2} – \frac{A}{2}$

Or $D_m = \pi – 2A$

Hence option (A) is the correct answer

Resources:

1. Refraction by a Prism
2. Solution on toppr.com
3. Video Solution